I -- INTRODUCTION
On 21 December 1988, Pan Am Flight 103 from London to New York exploded 31,000ft over Lockerbie, 38 minutes after take-off from London. The 259 people on board the Boeing 747 were killed, along with 11 people on the ground. [1, 2]
The trial court found that the bomb which destroyed PA103 was composed of about one pound of plastic explosive contained within a Toshiba RT-SF16 radio cassette player which had been placed inside a brown hard-shell Samsonite suitcase known as the primary suitcase. [3, 4, 5]
The trial court also found that the primary suitcase had been placed on board Air Malta flight KM180 from Malta to Frankfurt where it was transferred via the baggage system to Pam Am flight 103A from Frankfurt to Heathrow where it was loaded in container AVE 4041 in position 14L of PA103. [6]
From the known properties of the explosive, namely SEMTEX H, and the mechanical features of the plane fuselage, it can be demonstrated that the verdict is scientifically implausible. In order to reach the widest audience, the author intends to explain in the simplest possible terms the scientific implausibility of the Lockerbie verdict. [7]
II -- OVERVIEW OF THE METHODOLOGY
According to a widely accepted theory, the response of a mechanical structure to a shock wave will depend on two criteria, namely the critical time of the structure exposed to the blast and the critical positive impulse generated by the blast. [8, 9]
In a seminal paper, R. G. S. Sewell and G. F. Kinney explained that a structure will fail if two conditions are met simultaneously. The impulse produced by the explosion must exceed the critical impulse of the material composing the structure and the duration of the positive phase of the impulse must be shorter than the critical time associated with the mechanical structure. [10]
We will now show that although the time duration is indeed considerably shorter than the time duration of the impulse, the value of the positive impulse generated by the explosion of one pound of plastic located inside the container is far below the critical impulse of the material composing the skin of the Boeing 747 at the location of the primary fracture, namely AA 2024-T3. [11]
III -- DEFINITIONS
Following an explosion, a shock wave expands spherically until meeting an obstacle. While expanding freely, the following sequence of events occurs. At first, the pressure rises suddenly above ambient pressure. Then, the pressure drops exponentially, eventually to the original ambient pressure.
Impulse -- The integral of the pressure between the times associated with these two events is known as the positive impulse per unit area or simply the impulse.
Time Duration -- The interval between these two events is known as the time duration of the positive impulse per unit area, or time duration.
Critical Velocity – As a structure is subjected to a series of impact tests of steadily increasing velocity, several transitions from one type to a different type of behavior occur. The velocity at which such a transition occurs is called critical velocity. For instance there exists a critical velocity at which permanent (“plastic”) deformation will first occur. The most important critical velocity in the context of this work is the velocity at which the specimen fractures at the point of impact.
Critical Impulse -- The critical impulse per unit area associated with the critical velocity of a given specimen is given by elementary considerations as Ic = ρ δ Vc, where ρ is the density of the target material, δ is the thickness of the material, and Vc is the critical velocity.
Critical Time – When a structure can be idealized as having a single degree of freedom capable of harmonic motion, which is the case at hand, the critical time of that structure is defined as one quarter of the period associated with the first natural mode of oscillation.
IV -- APPLICATION TO THE PAN AM 103 BOMBING
IV-1 --
CONSIDERATIONS REGARDING THE CRITICAL TIME
IV-1-1
DETERMINATION OF THE NATURAL FREQUENCY
At the location of the primary fracture, the fuselage of the 747 is made of 1/16 inch thick, 20 inches square AA 2024-T3 plates.
The frequency of the first mode of oscillation of a clamped, i.e. all edges fixed, rectangular flat plate with short edge a long edge b and thickness t is given by the following equation:
f =
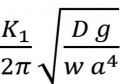
For a/b = 1, K1 = 36.0. D = E t3/ 12 (1- ν3) where E is the modulus of elasticity and ν the Poisson number. [12] The above equation predicts a frequency of 52 Hz.
Computer simulations confirm the value of this frequency. SOLID 45 and SOLID 185 both predict a frequency of 57 Hz. [13] Finally, the extrapolation of experimental data regarding the first natural mode of oscillation of a 6 by 6 inches AA 2024-T3 clamped plate predict a natural frequency of 44 Hz. [14]
Together, the four above methods estimate a natural frequency of about 50 Hz and, thus, a period of 20 ms and a critical time of 5 ms.
IV-1-2
DETERMINATION OF THE TIME DURATION
At two feet or less from the center of the explosion, the time duration associated with one pound of plastic is significantly less than 1 ms. [15, 16]
IV-1-3
CONCLUSION REGARDING THE TIME CRITERIA
Consequently, it can be safely concluded that the time duration of the blast was indeed significantly shorter than the critical time of the structure. We will now turn our attention to the second criteria which must also be met to ensure fracture.
IV-2 --
CONSIDERATIONS REGARDING CRITICAL IMPULSE AND BLAST IMPULSE
IV-2-1 --
CONSIDERATIONS REGARDING THE CRITICAL IMPULSE
Based on experimental determination of the critical velocity for AA 2024-T3, namely 62 m/s, the critical impulse of the target material is estimated at about 50 psi-ms. [17]
As first demonstrated by Von Karman, the critical velocity may also be derived from the slope of the stress-strain curve. A calculation based on a Bi-Linear model of the stress-strain curve of AA 2024 T3 yields a critical velocity of 65 m/s and thus a critical impulse of 52 psi-ms. [18]
The critical velocity may also be determined by another method if the speed of sound in the alloy and the dynamic yield strength of the target material (fuselage) alloy are known. Indeed, the critical impulse is given by elementary consideration as Ic = ρ σy/ S where σy is the dynamic yield, namely 140,000 psi [19] and S is the speed of sound in the material, namely 5140 m/s [20].
A strain rate of 106s-1 predicts a dynamic increase factor of the yield strength of 2.75 and thus dynamic yield strength of 120,000 psi (880 MPa). The value of the dynamic increase factor is very insensitive to the exact value of the strain rate. For instance, a strain rate of 107s-1 would predict a dynamic increase factor of about 3, barely a 10% increase in spite of a factor of 10 increase in the strain rate.
Using the above equation, the experimentally measured speed of sound in AA 2024-T3 and the calculated value of the dynamic yield strength, we find a value for the critical impulse of about 51 psi-ms. [21]
Finally, the speed of sound in AA 2024-T3 can also be predicted from the known value of the modulus of elasticity and the density. [22]
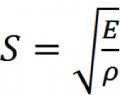
This provides a four independent prediction for the value of the critical impulse, namely 51 psi-ms. [23]
For the sake of thoroughness, we shall briefly address two minor issues. Regarding the thickness of the plate, as correctly pointed in the Aircraft Accident Report N2/90, the contributions of the stringers and frames are considered to be equivalent of a reduction of stress in the skins by 20%, corresponding to an increase in skin thickness from 0.064 inches to 0.080 inches. [24] This increase was taken into account in the aforementioned estimates.
Regarding the effect of the lower temperature at cruising altitude, the Johnson-Cook constitutive model predicts a small increase, of the order of a few percent, of the critical impulse of the specimen. [25, 26]
It is noteworthy that all four independent calculations of the critical impulse of AA 2024-T3 yield a remarkably consistent value of about 50 psi-ms.
IV-2-2 --
CONSIDERATIONS REGARDING THE BLAST IMPULSE
The outside wall of the AVE 4041 container was located at 16 inches from the skin of the plane. At this closest possible distance in the light most favorable to the original investigators, experimental data indicate that one pound of explosive will generate a positive impulse of less than 20 psi-ms against the fuselage. [27]
IV-2-3 –
CONCLUSION REGARDING THE IMPULSE CRITERIA
As this value is well below the critical impulse calculated above, namely 50 psi-ms, we have little choice but to conclude that the Lockerbie verdict is scientifically implausible. The fact that SEMTEX-H has an energy content per mass slightly higher than TNT, namely 4.9 vs 4.6 Mega Joule per kilogram, does not in any way affect our conclusion.
V -- ADDITIONAL COMMENTS
In the immediate aftermath of the tragedy, researchers at the Center for Explosives Technology Research in Socorro, New Mexico, estimated that up to 30 pounds of explosive was needed to destroy a Boeing 747 if the explosion had occurred in the container. [28] We agree with that estimate.
On the other hand, RARDE scientists concluded that one pound of explosive was sufficient to fracture the skin of the 747 at a distance of 25 inches, a distance determined using the theory of Mach stem formation. [29]
Although we endorse the view that the theory of Mach stem formation allows for the determination of the standoff distance, we respectfully, but categorically, disagree with the conclusions of the RARDE reports.
Regarding Mach stem formation, RARDE scientists incorrectly assumed that the formation occurs at about 20 degrees, while it realistically occurs at about 40 degrees. Had the correct angle been used, original calculations would have demonstrated the location of the bomb to be approximately 10 inches from the skin of the plane and, thus, clearly outside the container.
The basis by why RARDE scientists concluded that one pound of explosive could fracture AA 2024-T3 at a distance of 2 feet was from extrapolation of experimental data to less than 3 feet scaled distance. Such extrapolation is, however, known to be inappropriate because for such small distance, explosion physics are significantly different. [30]
Finally, following the initial phase of overpressure, the pressure beyond a critical distance mentioned above actually temporarily drops below the original ambient pressure before eventually returning to it, at which point the shock wave has degenerated into a sound wave.
As a result of being exposed to a push and then a pull by the positive and negative phase of the impulse, a frame will sometimes take the shape of a S with the S lying in a geometric plane determined by the original frame and the center of the explosion. A visual examination of a frame near the primary fracture indicates that the explosive must have been located very near the fuselage and not inside the AVE 4041 container.
VI -- CONCLUSION
As the explosion of one pound of SEMTEX H inside the luggage container does not generate a blast wave sufficiently powerful to fracture the skin of the fuselage, we have little choice but to conclude that the verdict appears scientifically implausible.
NOTES AND REFERENCES
1. Jetliner carrying 258 to U.S. crashes in Scottish town, New York Times, Dec 22 1988
2. Let us give Lord Sutherland, Lord Coulsfield and Lord Maclean some credit. After hearing 230 witnesses and studying 621 exhibits during 84 days of evidence, spread over eight months, the three judges of the Lockerbie trial almost established correctly the date of the worst act of terror in the UK. In the first line of the first paragraph of the most expensive verdict in history (₤80m), they wrote: "At 1903 hours on 22 December 1988 Pan Am flight 103 fell out of the sky."
3. According to the indictment issued in Nov. 1991, the bomb was composed of 10 to 14 ounces of plastic explosive.
4. Opinion of the Judges -- § 7 and 11
5. At the trial, RARDE scientist A. Feraday testified that the maximum amount of Semtex that could be fitted in a functioning Toshiba radio of the type used in the bombing of PA103 was 650 grams.
Q Could you, for instance, have loaded 450 grams?
A Yes, I could have loaded 450 grams in there.
Q Could you have loaded more?
A I could have loaded more in there, yes, sir.
Q What would be the maximum quantity of Semtex that you could have loaded in the fashion shown to us?
A In order for it not to be visible from the outsides -- that is, to not be seen through the slots at the back of the case -- my opinion is that anything greater than about 650 grams would have been visible. That's approximately a pound and a half, absolute maximum. I would stress that is absolute maximum. It is visible at one and a half pounds.
6. Opinion of the Judges -- § 17
7. This article is a summary of a collaborative work of the author with Mr. V. Bastidas and Mr. William Tobin.
8. Ngo T, Mendis P.and Ramsay J.: Blast loading and Blast effects on Structure. U. of Melbourne. 2007
9. Li Q. M. and Meng H.: Pressure – impulse diagram for blast Load. 2002
10. Kinney, G. F. “Response of Structures to Blast: A New Criterion” US Naval Postgraduate School – 1968
11.
Alloy 2024-T3 sheet and plate
12. Leissa A. W.: Vibration of plates, NASA SP 160, National Aeronautics and Space Administration, 1969.
13. In both simulations, triangular meshing was used. LS-DYNA3D - Finite element code, V940, Livermore Software Technology Corporation.
14. Bleeker Kellie, Dynamic Response of a Square Clamped Plate. Hope College Summer Research 2000.
15. Esparza, E. “Blast Measurements and Equivalency for Spherical Charges at Small Scaled Distances”. Int. J. Impact Engineering Vol. 4, No. 1, pp. 23-40, 1986.
16. Muzychuk E., Mayseless M. and Belsky I.: The influence of Post detonation burning process on blast wave parameters in air. 22nd International Ballistics Symposium, 2005.
17. Rinehart, J. S. “Behavior of Metals under Impulsive Loads”. Dover Publications, INC., New York. 1954.
18. Veldman R. L. “Effects of pre-pressurization on blast response of clamped aluminum plates”. International Journal of Impact Engineering vol. 32 pg. 1678-1695. 2005
19. The value is quoted in Kinney, G. F. “Response of Structures to Blast: A New Criterion” US Naval Postgraduate School – 1968
20 The value is quoted in NASA Technical Memorandum, NASA TM-103565, SINGLE WALL PENETRATION EQUATIONS by K.B. Hayashida and J.H. Robinson, December 1991
21. E = 72 GPa and ρ = 2770 kg / m3
22. Bastidas Poveda Victor. Thesis: Material Sciences and Explosives. Physics Department, University of Los Andes, Bogota. 2008.
23. Ibid
24. Aircraft Accident Report No 2/90 (EW/C1094). Report on the accident to Boeing 747-121, N739PA at Lockerbie, Dumfriesshire, Scotland on 21 December 1988. United Kingdom Air Accidents Investigation Branch.
25. M. Sasso, G. Newaz. “Material characterization at high strain rate by Hopkinson bar tests and finite element optimization”. Materials Science and Engineering A 487 (2008) 289-300. 2007.
26. R. Smerd. “High strain rate tensile testing of automotive aluminum alloy sheet”. International Journal of Impact Engineering 32 (2005) 541-560. 2005.
27. Esparza, E. “Blast Measurements and Equivalency for Spherical Charges at Small Scaled Distances”. Int. J. Impact Engng Vol. 4, No. 1, pp. 23-40, 1986.
28. Experts Say Bombing showed Technical Skill, NYT, Dec. 29 1988
29. Aircraft Accident Report No 2/90 (EW/C1094). Report on the accident to Boeing 747-121, N739PA at Lockerbie, Dumfriesshire, Scotland on 21 December 1988. United Kingdom Air Accidents Investigation Branch. Appendix G
30. Cooper P. W.: Explosives Engineering, Wiley VCH. 1996
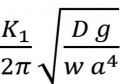 For a/b = 1, K1 = 36.0. D = E t3/ 12 (1- ν3) where E is the modulus of elasticity and ν the Poisson number. [12] The above equation predicts a frequency of 52 Hz.
Computer simulations confirm the value of this frequency. SOLID 45 and SOLID 185 both predict a frequency of 57 Hz. [13] Finally, the extrapolation of experimental data regarding the first natural mode of oscillation of a 6 by 6 inches AA 2024-T3 clamped plate predict a natural frequency of 44 Hz. [14]
Together, the four above methods estimate a natural frequency of about 50 Hz and, thus, a period of 20 ms and a critical time of 5 ms.
IV-1-2 DETERMINATION OF THE TIME DURATION
At two feet or less from the center of the explosion, the time duration associated with one pound of plastic is significantly less than 1 ms. [15, 16]
IV-1-3 CONCLUSION REGARDING THE TIME CRITERIA
Consequently, it can be safely concluded that the time duration of the blast was indeed significantly shorter than the critical time of the structure. We will now turn our attention to the second criteria which must also be met to ensure fracture.
IV-2 -- CONSIDERATIONS REGARDING CRITICAL IMPULSE AND BLAST IMPULSE
IV-2-1 -- CONSIDERATIONS REGARDING THE CRITICAL IMPULSE
Based on experimental determination of the critical velocity for AA 2024-T3, namely 62 m/s, the critical impulse of the target material is estimated at about 50 psi-ms. [17]
As first demonstrated by Von Karman, the critical velocity may also be derived from the slope of the stress-strain curve. A calculation based on a Bi-Linear model of the stress-strain curve of AA 2024 T3 yields a critical velocity of 65 m/s and thus a critical impulse of 52 psi-ms. [18]
The critical velocity may also be determined by another method if the speed of sound in the alloy and the dynamic yield strength of the target material (fuselage) alloy are known. Indeed, the critical impulse is given by elementary consideration as Ic = ρ σy/ S where σy is the dynamic yield, namely 140,000 psi [19] and S is the speed of sound in the material, namely 5140 m/s [20].
A strain rate of 106s-1 predicts a dynamic increase factor of the yield strength of 2.75 and thus dynamic yield strength of 120,000 psi (880 MPa). The value of the dynamic increase factor is very insensitive to the exact value of the strain rate. For instance, a strain rate of 107s-1 would predict a dynamic increase factor of about 3, barely a 10% increase in spite of a factor of 10 increase in the strain rate.
Using the above equation, the experimentally measured speed of sound in AA 2024-T3 and the calculated value of the dynamic yield strength, we find a value for the critical impulse of about 51 psi-ms. [21]
Finally, the speed of sound in AA 2024-T3 can also be predicted from the known value of the modulus of elasticity and the density. [22]
For a/b = 1, K1 = 36.0. D = E t3/ 12 (1- ν3) where E is the modulus of elasticity and ν the Poisson number. [12] The above equation predicts a frequency of 52 Hz.
Computer simulations confirm the value of this frequency. SOLID 45 and SOLID 185 both predict a frequency of 57 Hz. [13] Finally, the extrapolation of experimental data regarding the first natural mode of oscillation of a 6 by 6 inches AA 2024-T3 clamped plate predict a natural frequency of 44 Hz. [14]
Together, the four above methods estimate a natural frequency of about 50 Hz and, thus, a period of 20 ms and a critical time of 5 ms.
IV-1-2 DETERMINATION OF THE TIME DURATION
At two feet or less from the center of the explosion, the time duration associated with one pound of plastic is significantly less than 1 ms. [15, 16]
IV-1-3 CONCLUSION REGARDING THE TIME CRITERIA
Consequently, it can be safely concluded that the time duration of the blast was indeed significantly shorter than the critical time of the structure. We will now turn our attention to the second criteria which must also be met to ensure fracture.
IV-2 -- CONSIDERATIONS REGARDING CRITICAL IMPULSE AND BLAST IMPULSE
IV-2-1 -- CONSIDERATIONS REGARDING THE CRITICAL IMPULSE
Based on experimental determination of the critical velocity for AA 2024-T3, namely 62 m/s, the critical impulse of the target material is estimated at about 50 psi-ms. [17]
As first demonstrated by Von Karman, the critical velocity may also be derived from the slope of the stress-strain curve. A calculation based on a Bi-Linear model of the stress-strain curve of AA 2024 T3 yields a critical velocity of 65 m/s and thus a critical impulse of 52 psi-ms. [18]
The critical velocity may also be determined by another method if the speed of sound in the alloy and the dynamic yield strength of the target material (fuselage) alloy are known. Indeed, the critical impulse is given by elementary consideration as Ic = ρ σy/ S where σy is the dynamic yield, namely 140,000 psi [19] and S is the speed of sound in the material, namely 5140 m/s [20].
A strain rate of 106s-1 predicts a dynamic increase factor of the yield strength of 2.75 and thus dynamic yield strength of 120,000 psi (880 MPa). The value of the dynamic increase factor is very insensitive to the exact value of the strain rate. For instance, a strain rate of 107s-1 would predict a dynamic increase factor of about 3, barely a 10% increase in spite of a factor of 10 increase in the strain rate.
Using the above equation, the experimentally measured speed of sound in AA 2024-T3 and the calculated value of the dynamic yield strength, we find a value for the critical impulse of about 51 psi-ms. [21]
Finally, the speed of sound in AA 2024-T3 can also be predicted from the known value of the modulus of elasticity and the density. [22]
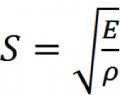 This provides a four independent prediction for the value of the critical impulse, namely 51 psi-ms. [23]
For the sake of thoroughness, we shall briefly address two minor issues. Regarding the thickness of the plate, as correctly pointed in the Aircraft Accident Report N2/90, the contributions of the stringers and frames are considered to be equivalent of a reduction of stress in the skins by 20%, corresponding to an increase in skin thickness from 0.064 inches to 0.080 inches. [24] This increase was taken into account in the aforementioned estimates.
Regarding the effect of the lower temperature at cruising altitude, the Johnson-Cook constitutive model predicts a small increase, of the order of a few percent, of the critical impulse of the specimen. [25, 26]
It is noteworthy that all four independent calculations of the critical impulse of AA 2024-T3 yield a remarkably consistent value of about 50 psi-ms.
IV-2-2 -- CONSIDERATIONS REGARDING THE BLAST IMPULSE
The outside wall of the AVE 4041 container was located at 16 inches from the skin of the plane. At this closest possible distance in the light most favorable to the original investigators, experimental data indicate that one pound of explosive will generate a positive impulse of less than 20 psi-ms against the fuselage. [27]
IV-2-3 – CONCLUSION REGARDING THE IMPULSE CRITERIA
As this value is well below the critical impulse calculated above, namely 50 psi-ms, we have little choice but to conclude that the Lockerbie verdict is scientifically implausible. The fact that SEMTEX-H has an energy content per mass slightly higher than TNT, namely 4.9 vs 4.6 Mega Joule per kilogram, does not in any way affect our conclusion.
This provides a four independent prediction for the value of the critical impulse, namely 51 psi-ms. [23]
For the sake of thoroughness, we shall briefly address two minor issues. Regarding the thickness of the plate, as correctly pointed in the Aircraft Accident Report N2/90, the contributions of the stringers and frames are considered to be equivalent of a reduction of stress in the skins by 20%, corresponding to an increase in skin thickness from 0.064 inches to 0.080 inches. [24] This increase was taken into account in the aforementioned estimates.
Regarding the effect of the lower temperature at cruising altitude, the Johnson-Cook constitutive model predicts a small increase, of the order of a few percent, of the critical impulse of the specimen. [25, 26]
It is noteworthy that all four independent calculations of the critical impulse of AA 2024-T3 yield a remarkably consistent value of about 50 psi-ms.
IV-2-2 -- CONSIDERATIONS REGARDING THE BLAST IMPULSE
The outside wall of the AVE 4041 container was located at 16 inches from the skin of the plane. At this closest possible distance in the light most favorable to the original investigators, experimental data indicate that one pound of explosive will generate a positive impulse of less than 20 psi-ms against the fuselage. [27]
IV-2-3 – CONCLUSION REGARDING THE IMPULSE CRITERIA
As this value is well below the critical impulse calculated above, namely 50 psi-ms, we have little choice but to conclude that the Lockerbie verdict is scientifically implausible. The fact that SEMTEX-H has an energy content per mass slightly higher than TNT, namely 4.9 vs 4.6 Mega Joule per kilogram, does not in any way affect our conclusion.